MAT 2040

你或许会更想去 Notekit 看这份笔记

​MAT 2040​ Course Content

• 进考场之前看什么

  • Det = 0 说明是 singular 也就是 not invertible $$Ax=0$$ has infinite many solution 行列向量是线性相关的
    Det != 0 说明是 nonsingular 也就是 invertible $$ Ax = 0 $$ has only a trivial solution 说明是满秩的(但非方矩阵满秩不一定推出 invertible) 行列向量是线性无关的

  • ((Property 16.6 (Determinants of Three Elementary Matrices)
    第一类：行交换 $$det=-1$$
    第二类：行标量乘 $$det=\alpha$$
    第三类：一行加另一行标量乘 $$det=1$$ ))

  • ((Definition 16.13 Adjoint Matrix
    在原矩阵 $$a_{ij}$$ 位置放 Cofactor $$A_{ij}=(-1)^{i+j}det(M_{ij})$$ 再 Transpose 就得到了 Adjoint Matrix $$A\ adj(A)=det(A)I_n$$ $$If\ det(A)\neq 0, A^{-1}=\frac{1}{det(A)}adj(A)$$ -> method to find $$A^{-1}$$ ))

  • ((Linear transformation
    线性变换是一种保持向量加法和标量乘法的映射. 这意味着：
    向量的加法在变换前后保持一致.
    标量乘法在变换前后保持一致.))

  • ((Example 17.14
    二维平面起点为原点的逆时针旋转： $$A=\left[\begin{matrix}\cos\theta & -\sin\theta\\ \sin\theta & \cos\theta\end{matrix}\right]\\ L\left(\left[\begin{matrix}x\\ y\end{matrix}\right]\right)=A\left[\begin{matrix}x\\ y\end{matrix}\right]=\left[\begin{matrix}x\cos\theta-y\sin\theta\\ x\sin\theta+y\cos\theta\end{matrix}\right]$$ 二维平面起点为原点的顺时针旋转 $$B=\left[\begin{matrix}\cos\theta & \sin\theta\\ -\sin\theta & \cos\theta\end{matrix}\right]\\ L\left(\left[\begin{matrix}x\\ y\end{matrix}\right]\right)=B\left[\begin{matrix}x\\ y\end{matrix}\right]=\left[\begin{matrix}xcos\theta+ysin\theta\\ -xsin\theta+ycos\theta\end{matrix}\right]$$ ))

  • ((Theorem 18.1 (Matrix Representation for General Vector Spaces) $$L: V\to W\,\,[L({\bf u})]_w=A[{\bf u}]_v,\forall{\bf u} \in V$$ ，转换矩阵 $$A$$ 每列为 $$V$$ 基底提前经 $$L$$ 变换后转到 $$W$$ ))

  • ((Theorem 19.17 (Fundamental Subspaces Theorem) $$Null(A)=Col(A^T)^\perp=Row(A)^\perp$$ $$Null(A^T)=Col(A)^\perp=Row(A^T)^\perp$$ ))

  • $$dim\ S+dim\ S^\perp = n$$

  • $$A^T(\mathbf{b}-A\hat{\mathbf{x}})=0\\ A^TA\hat{\mathbf{x}}=A^T\mathbf{b}$$ (Normal Equation)

  • 最小二乘估计

  • ((Definition 21.15 (Orthogonal Matrix) $$Q\in \R^{n\times n}$$ ，若 $$Q$$ 的列向量是 $$\R^n$$ 中的一个OrthonormalSet，则 $$Q$$ 是OrthogonalMatrix)) $$Q^{-1}=Q^T$$

  • $$A=QR$$ 要求 $$\text{rank}(A)=n$$ $$Q$$ 为 Orthogonal Matrix，是经Gram-Schmidt 得到的， $$R=Q^{-1}A=Q^TA$$

  • 对于一个可QR分解的矩阵，算Normal Equation有简化方法((Theorem: $$A^TA\hat{x}=A^T{\bf b}$$ $$R^TR\hat{x}=R^TQ^Tb$$ Finally: $$R\hat{x}=Q^T\mathbf{b}$$ $$\hat{x}=R^{-1}Q^T\mathbf{b}$$ ))

  • Characteristic Equation $$p_A(\lambda)=\text{det}(A-\lambda I)=0$$

  • $$\text{Null}(A-\lambda I)$$ is called the eigenspace corresponding to $$\lambda$$

  • $$\displaystyle\text{det}(A)=\prod_{i=1}^n \lambda_i$$ 行列式=特征值积 $$\displaystyle\sum_{i=1}^n a_{ii}=\sum_{i=1}^n\lambda_i=tr(A)$$ 迹=特征值和

  • (( $$A$$ is nonsingular and $$\lambda$$ is the eigenvalue of $$A$$ , Then $$\iff \lambda^{-1}$$ is the eigenvalue of $$A^{-1}$$ ))

  • 相似矩阵有相同特征值

  • 不同eigenvalue对应的eigenvector线性独立

  • A $$n\times n$$ matrix $$A$$ is diagonalizable iff $$A$$ has $$n$$ linearly independent eigenvectors

  • 对称矩阵的一定有n个不等的eigenvalues，所对应向量相互垂直

  • Diagonalize: $$D=Q^{-1}AQ$$ ，求 $$D$$ 的方法： $$\left[\begin{matrix}\lambda_1&0&0\\0&\lambda_2&0\\0&0&\lambda_3\end{matrix}\right]$$ ，求 $$Q$$ 的方法：把 eigenvalue 对应的 eigenvector 作为列向量组成矩阵；对于对称矩阵有 $$D=Q^TAQ=\lambda_1\mathbf{q}_1\mathbf{q}_1^T+\cdots+\lambda_n\mathbf{q}_n\mathbf{q}_n^T$$

  • $$f({\bf x})={\bf x}^TA{\bf x}$$ 根据是否与 $${\bf x}$$ 的取值无关而>(=) <(=) 0 有 positive (semi)definite & negative (semi)definite & indefinite

  • Postive Definite 等价 Eigenvalues全正 等价 LeadingPrincipalMinors全正 等价 $$A=C^2$$ 等价 $$A=LL^T$$ (Lower Triangular 对角>0) 等价 $$A=LDL^T$$

  • ((Gram-Schmidt Process 格拉姆-施密特正交化))

• Slide 1 - Linear Systems and Matrices I

  • Notations $$\vec{u} \to Row\ Vector\\ \underline{u}\to Column\ Vector$$

  • Special Matrix $$O \to Zero\ Matrix \\ I\to Identity\ Matrix\\ \vec{0} \to Zero\ Vector$$

  • Definition 1.17 (Row-Equivalent Matrices) Two matrices are said to be row equivalent if one can obtained from the other by a sequence of elementary row operations.

  • Theorem 1.18 (Equivalent Linear Systems) Consider two linear systems. Row operations for the augmented matrix preserve the solution set of the linear system.

  • Forward Elimination -> the upper triangular matrix (至少会得到一个 Row Echelon Form)
    Backward substitution -> Solution

• Slide 2 - Linear Systems and Matrices II Slide02.pdf

  • Gaussian Elimination + Back Substitution

  • Definition 2.1 (Row Echelon Form)
    前导零更多的行靠下 & 全0的行在最下

  • Reduced row echelon form (RREF)
    是 Row Echelon Form & 每行前导为1 & 前导1为整列唯一非0

  • $$\#\ non\ zero\ rows=\#\ of\ pivot\ columns=\#\ of\ leading\ 1's$$

  • -> Upper triangular form 一定是 Row echelon form，但是 Row echelon form 不一定是 Upper triangular form

• Slide 3 - Linear Systems and Matrices III Slide03(1).pdf

  • Consistence $$Consistent\to 有解\\ Inconsistent\to 无解$$

  • Consistent 等价 （Augmented Matrix 的最右列不是一个 Pivot Column）

  • 当 Pivot 数与未知数的数量相等时有唯一解. 否则有无数解，若有 $$r$$ 个 Pivot，可有 $$n-r$$ 个 Free/Independent Variables

  • 一个 Linear Equations System 有唯一解、无数解或无解

  • 当我们有一行 $$\begin{matrix}[ 1 & 0 & 3 & -2 & | & 4 ]\end{matrix}$$ ，我们写 $$x_1=4-3x_3+2x_4$$

  • Homogeneous System即 $$A\boldsymbol{x} = \boldsymbol{0}$$

    • 总是有解因为 $$\boldsymbol{x}=\boldsymbol{0}$$ 总是一个解 这个解叫 Trivial Solution

    • Underdetermined homogeneous systems 有无数个解 $$\#\ of\ pivot\ columns=\#\ of\ nonzero\ rows\leq m \lt n$$

  • Underdetermined consistent systems 有无数个解 $$\#\ of\ pivot\ columns=\#\ of\ nonzero\ rows\leq m\lt n$$

• Slide 4 - Matrices Algebra I Slide04(1).pdf

  • Set of Matrices $$\R^{m\times n}\ \Complex^{m\times n}$$

  • Set of Column Vectors $$\R^n=\R^{n\times 1}\ \Complex^n=\Complex^{n\times 1}$$

  • 矩阵相等 每一项相等

  • 矩阵相加 row=row col=col

  • 标量乘 用标量乘每一项

  • Zero Matrix 每一项都是 $$0\ O_{m\times n}$$

  • 列向量 行向量

  • 矩阵加和标量乘均满足：交换率 结合率 分配率（标量乘）

  • 矩阵乘向量
    用每一行向量乘以该向量，得新行向量
    || alinear combination of column vectors $$a_1,a_2,\cdots,a_n$$ with weights $$u_1,\cdots,u_n$$

    • 满足分配律，满足 $$A(\alpha \boldsymbol{x})=(\alpha A)\boldsymbol{x}=\alpha(A \boldsymbol{x})$$

  • 

  • Equivalent Condition for a Consistent Linear SystemThe linear system $$A\boldsymbol{x} = \boldsymbol{b}$$ is consistent if and only if $$\boldsymbol{b}$$ is a linear combination of the column vectors of $$A$$ .

  • Matrix Product $$A \times B = [A\boldsymbol{b}_1,\cdots,A\boldsymbol{b}_r] =C (A \in \R^{m\times n}, B\in \R^{n\times R})\\ c_{ij} = \sum^{n}_{k=1} a_{ik}b_{kj}=\vec{a}_i\boldsymbol{b}_j$$ 用 A 的行乘 B 的列，所以 A 每行元素与 B 每列元素相等，也就是说 A 的列 = B 的行

    • 注意⚠️ 不满足交换，也不可等式两边约： $$AB=AC$$ 不说明 $$B=C$$

    • 满足分配律，同时满足 $$\alpha(AB)=(\alpha A)B=A(\alpha B)$$

• Slide 5 - Matrices Algebra II Slide05.pdf

  • $$AB=O$$ does not imply that $$A=O$$ or $$B=O$$

  • Diagonal Matrix $$diag(1,2,-5,3)=\left[\begin{matrix} 1&0&0&0\\0&2&0&0\\0&0&-5&0\\0&0&0&3\end{matrix}\right] \\ I_3=\left[\begin{matrix}1&0&0\\0&1&0\\0&0&1\end{matrix}\right]$$

  • Multiplication of Identity Matrix $$ AI_n = I_nA = A,\ \forall A \in \R^{n\times n} $$

  • Transpose of Matrix $$b_{ji}=a_{ij}$$ $$(A+B)^T=A^T+B^T\\ (\alpha A)^T=\alpha A^T\\ (A^T)^T=A\\ (AB)^T=B^TA^T$$

  • Symmetric Matrix $$A=A^T$$

  • Skew-symmetric Matrix $$A^T=-A$$

  • Any square matrix can be written as a sum of a symmetric matrix and a skew-symmetric matrix. $$A=\frac{A+A^T}{2}+\frac{A-A^T}{2}$$

  • Invertible Matrixalso called nonsingular or nondegenerate matrices
    Matrix inverse isunique $$AB=BA=I_n\\ B=A^{-1}\\ \boldsymbol{x}=A^{-1}\boldsymbol{b}$$

    • Matrix Inverse of a Matrix Transpose $$(A^T)^{-1}=(A^{-1})^T$$

    • Matrix Inverse of a Scalar Multiple $$(\alpha A)^{-1}=\frac{1}{\alpha}A^{-1}$$

    • Matrix Inverse of a Matrix Inverse $$(A^{-1})^{-1}=A$$

    • Matrix Inverse of Matrices Product $$(AB)^{-1}=B^{-1}A^{-1}$$

• Slide 6 - Matrix partition and elementary matrix Slide06.pdf

  • 

  • 

  • Elementary MatricesPerformexactly onetype of elementary row operations to an identity matrix. 只能一次操作

    • Type I: 行交换 Row Exchange Matrix

    • Type II: 行标量乘

    • Type III: 行+标量乘行

    • For a given matrix $$A$$ , performing elementary row operation for $$A$$ is equivalent topremultiplying $$A$$ by the corresponding elementary matrix.

    • Elementary Matrices are Invertible and Their Inverse are also Elementary Matrices $$E_{R_iR_j}^{-1}=E_{R_iR_j}\\ E^{-1}_{\alpha R_i}=E_{\frac{1}{\alpha}R_i}\ (\alpha \neq 0)\\ E^{-1}_{\beta R_i+R_j} = E_{-\beta R_i+R_j}$$

  • Permutation matrix
    Exactly one entry of $$1$$ in each row and each colomn and $$0$$ s elsewhere.
    不一定是 Elementary Matrix

• Slide 7 - LU decomposition Slide07.pdf

  • upper triangular matrix $$a_{ij}=0\ for\ i\gt j$$
    unit ~: 对角线为1

  • Lower triangular matrix $$a_{ij}=0\ for\ i\lt j$$
    unit ~: 对角线为1

  • $$With\ the\ same\ size\\ Upper\times Upper=Upper\\ Lower\times Lower=Lower$$

  • LU-decomposition $$[A|I] \to [U|B]\\ [B|I] \to [I|L]\\ A=LU$$

  • LDU decomposition for a nonsingular matrix

• Slide 8 - Find Matrix Inverse by using elementary martices/row operations Slide08.pdf

  • Row Equivalent Matrices 可以 Row Operation 得到（乘 Elementary Matrix）

  • Theorem 8.2 (Equivalent conditions for invertible matrix) $$A \in \R^{n \times n}$$ , the following are equivalent:

    • $$A$$ is invertible

    • The linear system $$Ax=0$$ has only a trivial solution

    • Matrix $$A$$ is row equivalent to $$I _n $$

    • $$A$$ is a product of elementary matrices

    • There exists an invertible matrix $$E \in \R^{n \times n}$$ such that $$EA=I_n$$

    • $$Ax=b$$ has a unique solution for any $$b$$
    • $$det(A) \neq 0$$

  • Method to find $$A^{-1}$$ $$[A|I] \xrightarrow{Gauss\ Jordan\ Elimination}[I|P], then\ P=A^{-1}$$

  • One-Sided Inverse Verification is Sufficient

  • The product $$AB$$ is nonsingular if and only if $$A$$ and $$B$$ are both nonsingular.

• Slide 9 - Vectors I Slide09.pdf

  • (Particular Solution and Homogeneous Solution)If $$w_0$$ is one solution of the linear system $$A\boldsymbol{x}=\boldsymbol{b}$$ , then we can treat $$w_0$$ as aparticular solutionfor $$A\boldsymbol{x}=\boldsymbol{b}$$ , The solution(s) of $$A\boldsymbol{x}=\boldsymbol{0}$$ are called thehomogeneous solutionsfor the corresponding linear system $$A\boldsymbol{x}=\boldsymbol{b}$$ .

• Slide 10 - Vectors II

  • Linearly independent 每一个系数都是0
    Linearly dependent 只要有一个系数不是0

    If S is a linearly dependent set, then each vector in S is a linear combination of other vectors in S.False 比如combination时系数为0的不能被表示 但一定有一些是可以被其他的 linear combination 表示的

    Any set containing the zero vector is linearly dependent.True 因为0前的系数可以是任何，满足有一个系数不是0

    Any nonempty subset of a linearly independent set of vectors $$\{v_1, . . . , v_n\}$$ is also linearly independent.True 如果有 subset 是 Linearly Dependent 的，那么保持这些系数不变，其他系数为 0，可以得到扩展后的集是 Linearly Dependent 的，所以所有的 subset 是 independent 的.

    Any nonempty subset of a linearly dependent set of vectors $$\{v_1, . . . , v_n\}$$ is also linearly dependent.False 比如一个 independent 加个 0 就是 dependent

• Slide 11 - Vectors Spaces Slide11.pdf

  • Vector Space $$\R\ \R^n\ \R^{m\times n}\ P_n\ C[a,b]$$ Additive Closure
    Scalar Closure

    8 Axiom
    加法
    A1 交换率
    A2 结合率
    A3 $$\boldsymbol{u} + \boldsymbol{0} = \boldsymbol{u}$$
    乘法
    A4 $$-\boldsymbol{u}=(-1)\boldsymbol{u}$$ A5 A6 向量部分可分配 标量部分可分配
    A7 标量部分可结合
    A8 标量 $$\times 1$$ 不变

  • Subspace $$\boldsymbol{0} \in H $$
    Additive Closure
    Scalar Closure

  • 

  • Linearly independent 每一个系数都是0
    Linearly dependent 只要有一个系数不是0

    • If S is a linearly dependent set, then each vector in S is a linear combination of other vectors in S.False 比如combination时系数为0的不能被表示 但一定有一些是可以被其他的 linear combination 表示的

    • Any set containing the zero vector is linearly dependent.True 因为0前的系数可以是任何，满足有一个系数不是0

    • Any nonempty subset of a linearly independent set of vectors $$\{v_1, . . . , v_n\}$$ is also linearly independent.True 如果有 subset 是 Linearly Dependent 的，那么保持这些系数不变，其他系数为 0，可以得到扩展后的集是 Linearly Dependent 的，所以所有的 subset 是 independent 的.

    • Any nonempty subset of a linearly dependent set of vectors $$\{v_1, . . . , v_n\}$$ is also linearly dependent.False 比如一个 independent 加个 0 就是 dependent

  • Spanning Set 是创建一个 Span 空间的来源向量
    A spans B 是说 $$B=Span(A)$$ A 是 B 的 Spanning Set
    B 是 A 的 Span

• Slide 12 - Basis and dimension Slide12.pdf

  • Basis $$u=\{\vec{u_1},\cdots,\vec{u_m}\}\\ u\ is\ linearly\ independent\\ Span(u)=V\\ So\ u\ is\ a\ basis\ of\ V$$

  • A vector set is linearly dependent if number of vectors in the set is larger than number of vectors in the basis

  • 维数够而且还线性独立就可以推出是基底

  • Transition Matrix between two bases
    想把用 u 表示的转为用 v，就用 v 来表示 u 的每一个向量 $$[x]_v=A[x]_u\ where\ the\ jth\ column\ of\ A\ is\ [u_j]_v\\ [x]_u=A^{-1}[x]_v\ where\ the\ jth\ column\ of\ A\ is\ [u_j]_v$$

• Slide 13 - Null Space, Column Space Slide13.pdf

  • The Null Space of $$A$$ is the solution set for $$A\vec{x}=\vec{0}$$ .

  • Span Colomn 就得到 Column Space

  • 找 Column Space 的方法是先求 Reduced Row Echelon Form，然后把 Pivot Column 对应的原矩阵列作为基底

    • 行变换会改变列空间

  • 找 Null Space 是用 Non-pivot column 对应的变量（free variable）表示其他的

  • $$dim(Col (A)) + dim(Null (A)) =n$$

• Slide 14 - Row Space and Rank Slide14.pdf

  • $$Row (A) = Col (A^T)$$ $$Row (A^T) = Col (A)$$

    其实是 行向量的 Transpose

  • Row operations preserves the row space

  • $$r= dim(Row (A)) = dim(Col (A))$$ is called the rank of $$A$$ , denoted by $$rank(A)$$ .

  • Full Rank Matrix $$rank(A) = min(m,n)$$

    • Rank-Nullity Theorem $$rank(A) +n(A) =n$$

• Slide 15 - Determinants I Slide15.pdf

  • Cofactor 是 -1 的几次方和一个 Minor 的乘积

  • Upper/Lower triangular 的 det 是对角线乘积

  • Determinant of Transpose $$det(A^T)=det(A)$$

  • Determinant with Equal Rows or Columns $$det(A)=0$$

• Slide 16 - Determinants II Slide16.pdf

  • Determinant for Row or Column Interchange $$B$$ is obtained by exchange exactly one row or column with another in $$A$$ . Then we have $$det(B)=-det(A)$$

  • Property 16.3 $$\alpha \neq 0\\A \xrightarrow{R_i\to \alpha R_i}B\ or\ A\xrightarrow{C_i\to \alpha C_i} B\\ Then\ det(B)=\alpha det(A)$$

  • Lemma 16.4 $$a_{i1}A_{j1}+\cdots+a_{in}A_{jn} =\begin{cases} \text{det}(A) & \text{if}\ i=j,\\ 0 & \text{if}\ i\neq j. \end{cases}$$

  • Property 16.5 $$A\xrightarrow{R_j\to \beta R_i+R_j} B (i\neq j)\\ Or\ C_j\to \beta C_i+C_j\\ Then\ \text{det}(B)=\text{det}(A)$$

  • Property 16.6 (Determinants of Three Elementary Matrices)
    第一类：行交换 $$det=-1$$
    第二类：行标量乘 $$det=\alpha$$
    第三类：一行加另一行标量乘 $$det=1$$

  • Determinants of Matrices Product
    If A and B are square matrices, $$det(AB)=det(A)det(B)$$

  • Property 16.12
    两等大矩阵仅一行或一列不同，行列式相加=那一行或一列相加其他不变的矩阵的行列式

  • Definition 16.13 Adjoint Matrix
    在原矩阵 $$a_{ij}$$ 位置放 Cofactor $$A_{ij}=(-1)^{i+j}det(M_{ij})$$ 再 Transpose 就得到了 Adjoint Matrix $$A\ adj(A)=det(A)I_n$$ $$If\ det(A)\neq 0, A^{-1}=\frac{1}{det(A)}adj(A)$$ -> method to find $$A^{-1}$$

• Slide 17 - Linear Transformation I Slide17.pdf

  • Linear transformation
    线性变换是一种保持向量加法和标量乘法的映射. 这意味着：
    向量的加法在变换前后保持一致.
    标量乘法在变换前后保持一致.

  • Property 17.5 (Property of Linear transformation) $$L(\boldsymbol{0}_V)=\boldsymbol{0}_W\\ L(\alpha_1\boldsymbol{u}_1+\cdots+\alpha_n\boldsymbol{u}_n)=\alpha L(\boldsymbol{u}_1)+\cdots+\alpha_n L(\boldsymbol{u}_n)\\ L(-\boldsymbol{u})=-L(\boldsymbol{u})$$

  • Definition 17.8 (Kernel of the Linear transformation)
    Let $$L$$ be a linear transformation from $$V$$ to $$W$$ , then the kernel of $$L$$ , denoted by $$ker(L)$$ is defined as $$ker(L) = \{v\in V | L(v) =0_W\}$$
    定义域V中被操作后能变0向量的所有向量集合叫 Kernel

  • Definition 17.9 (Image and Range)
    Let $$L$$ be a linear transformation from $$V$$ to $$W$$ and let $$S$$ be a subspace of $$V$$ , the image of $$S$$ , denoted by $$L(S)$$ , is dened by $$L(S) =\{\boldsymbol{w}\in W | \exists \boldsymbol{v}\in S, s.t.\ L(\boldsymbol{v}) = \boldsymbol{w}\}$$ The image of the entire vector space $$V$$ , i.e., $$L(V)$$ is called the range of $$L$$ .
    定义域V，子集S对应值域叫S的Image，整个定义域V对应值域叫L这个运算的range（其实也是V的Image）

  • Theorem 17.10
    Kernel是定义域的子空间，Image是值域的子空间

  • Theorem 17.12 (Matrix Representation for linear transformation between Eulerian vector spaces w.r.t. standard bases) $$L:\R^n \to \R^m$$ 所对应的矩阵 $$A\in \R^{m\times n}$$ ，满足列向量 $$\boldsymbol{a}_i=L(\boldsymbol{e}_i)$$ ， $$\boldsymbol{e}$$ 是 $$\R^n$$ 空间的标准基底.

  • Example 17.14
    二维平面起点为原点的逆时针旋转： $$A=\left[\begin{matrix}\cos\theta & -\sin\theta\\ \sin\theta & \cos\theta\end{matrix}\right]\\ L\left(\left[\begin{matrix}x\\ y\end{matrix}\right]\right)=A\left[\begin{matrix}x\\ y\end{matrix}\right]=\left[\begin{matrix}x\cos\theta-y\sin\theta\\ x\sin\theta+y\cos\theta\end{matrix}\right]$$ 二维平面起点为原点的顺时针旋转 $$B=\left[\begin{matrix}\cos\theta & \sin\theta\\ -\sin\theta & \cos\theta\end{matrix}\right]\\ L\left(\left[\begin{matrix}x\\ y\end{matrix}\right]\right)=B\left[\begin{matrix}x\\ y\end{matrix}\right]=\left[\begin{matrix}xcos\theta+ysin\theta\\ -xsin\theta+ycos\theta\end{matrix}\right]$$

• Slide 18 - Linear Transformation II Slide18.pdf

  • Theorem 18.1 (Matrix Representation for General Vector Spaces) $$L: V\to W\,\,[L({\bf u})]_w=A[{\bf u}]_v,\forall{\bf u} \in V$$ ，转换矩阵 $$A$$ 每列为 $$V$$ 基底提前经 $$L$$ 变换后转到 $$W$$

  • Theorem 18.4 (Similarity Result in general vector space) $$E$$ 、 $$F$$ 为空间 $$V$$ 两基底， $$S$$ 矩阵可从 $$F$$ 转 $$E$$ ， $$A$$ 是 $$L$$ 操作在 $$E$$ 的矩阵表示， $$B$$ 是 $$L$$ 操作在 $$F$$ 的矩阵表示， $$B=S^{-1}AS$$ 就是先从 $$F$$ 转 $$E$$ ，做完 $$L$$ 操作再转回来（从右往左看）

  • Definition 18.5 (Similar) $$A$$ 、 $$B$$ 为方阵， $$A$$ 、 $$B$$ Similar 是说 there exists a nonsingular matrix $$S$$ such that $$B=S^{-1}AS$$

• Slide 19 - Orthogonality Slide19.pdf

  • Let x and y are two vectors in $$\R^n$$ , then the product $$x^Ty$$ is called the scalar product 即类似点乘

  • Definition 19.1 (Euclidean Length)
    即模长

  • Definition 19.3 (Distance) $$||x-y||$$

  • Lemma 19.5 (Cauchy-Schwartz Inequality) $$|x^Ty|\le||x||\ ||y||$$

  • Theorem 19.6 (Scalar Product in terms of Vector Length) $$ x^Ty=||x||\ ||y||cos\theta, 0\le \theta \le \pi$$

  • Definition 19.7 (Orthogonal Vectors in $$\R^n$$ )
    Orthogonal <-> $$x^Ty=0$$

  • Theorem 19.9 (Pythagorean’s Law)
    Orthogonal <-> $$||x+y||^2=||x||^2+||y||^2$$

  • Definition 19.11 (Orthogonal Subspaces in $$\R^n$$ )
    两空间内任选向量都垂直
    可推出交集只有0向量

  • Definition 19.13 (Orthogonal Complement)
    同一空间内与子集 Y 中任一向量都垂直的所有向量集合叫 Y 的 Orthogonal Complement $$Y^{\perp}$$

  • Proposition 19.15 (Proposition of Orthogonal Complements)
    Y 是 $$\R^n$$ 的 subspace，那么 $$Y^\perp$$ 也是

  • Theorem 19.17 (Fundamental Subspaces Theorem) $$Null(A)=Col(A^T)^\perp=Row(A)^\perp$$ $$Null(A^T)=Col(A)^\perp=Row(A^T)^\perp$$

  • Theorem 19.19
    If $$S$$ is a subspace of $$\R^n$$ , then $$dim\ S+dim\ S^\perp = n$$
    and
    a basis for $$S$$ combined with a basis for $$S^\perp$$ is a basic for $$\R^n$$

• If $$S$$ is a subspace of $$\R^n$$ , $$(S^\perp)^\perp=S$$

• Slide 20 - Orthogonality II Slide20.pdf

  • Definition 20.1 (Direct sum)
    U V 是 W 的 subspace，任一 $$\mathbf{w}\in W$$ 可被写成唯一的 $$\mathbf{u}+\mathbf{v}$$ ，W 是空间 U 和 V 的 Direct Sum $$W=U \oplus V$$

  • Theorem 20.2 (Direct sum of $$\R^n$$ ) $$S$$ subspace of $$\R^n$$ , $$\R^n = S \oplus S^\perp$$

  • Definition 20.5 (Residual) 残差
    对于一个线性系统 $$A\mathbf{x}=\mathbf{b}(A\in \R^{m\times n},\mathbf{b}\in\R^m)$$ 中的每个 $$\mathbf{x}\in\R^n$$ ， $$r(\mathbf{x})=\mathbf{b}-A\mathbf{x}$$

  • Definition 20.6 (Least square solution)
    是 $$\hat{\mathbf{x}}$$ ，使残差最小. 即 $$||r(\hat{\mathbf{x}})||=min||r(\mathbf{x})||$$

  • Theorem 20.7 (Projection onto a Subspace) 投影
    对于任意向量 $$\mathbf{b}\in\R^m$$ ，我们能找到子空间 $$S$$ 内某向量 $$\mathbf{p}$$ 使得 $$1.\ \mathbf{b}-\mathbf{p}\in S^\perp$$ 即连线是空间垂直补集（三维即连线垂直于面） $$2.\ ||\mathbf{b}-\mathbf{y}||\ge||\mathbf{b}-\mathbf{p}||,\forall \mathbf{y}\in S$$ （原向量与投影共始点时末点连线长度最短）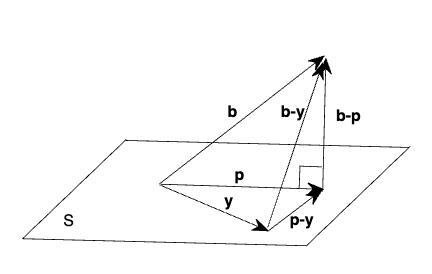

    • 

    • If $$\mathbf{b}\in S$$ , then the projection of $$\mathbf{b}$$ onto $$S$$ is just $$\mathbf{b}$$ .

    • Remark 2 对于一个线性系统 $$A\mathbf{x}=\mathbf{b}(A\in \R^{m\times n},\mathbf{b}\in\R^m)$$ ，当 $$\mathbf{x}=\hat{\mathbf{x}}(A\hat{\mathbf{x}}\text{ is the projection of }\mathbf{b}\text{ onto Col(A)})$$ ，残差最小.
      同时还有（ $$\forall \mathbf{y}\in Col(A)$$ ） $$\mathbf{b}-A\hat{\mathbf{x}}\perp A\hat{\mathbf{x}}-A\mathbf{y}\in Col(A)\\ ||\mathbf{b}-A\mathbf{y}||^2\ge||\mathbf{b}-A\hat{\mathbf{x}}||^2$$

  • Theorem 20.8 (Normal equations for the linear system) 对于一个线性系统 $$A\mathbf{x}=\mathbf{b}(A\in \R^{m\times n},\mathbf{b}\in\R^m)$$ ， $$\mathbf{b}$$ 在 $$Col(A)$$ 的投影是 $$\mathbf{p}$$ ， $$\mathbf{p}=A\hat{\mathbf{x}}\in Col(A)\\ \mathbf{b}-A\hat{\mathbf{x}} \in Col(A)^\perp=Null(A^T)\\ ||\mathbf{b}-A\mathbf{x}||\ge||\mathbf{b}-A\hat{\mathbf{x}}||$$ for any $$\mathbf{x}\in\R^n$$ $$A^T(\mathbf{b}-A\hat{\mathbf{x}})=0\\ A^TA\hat{\mathbf{x}}=A^T\mathbf{b}$$ (Normal Equation)

  • Theorem 20.9 (Unique Solution Condition for the Normal Equations)
    当 $$A\in \R^{m\times n}$$ 有 rank n，normal equations 有唯一解 $$\hat{\mathbf{x}}=(A^TA)^{-1}A^T\mathbf{b}$$

    • Projection matrix: $$\mathbf{p}=A\hat{\mathbf{x}}=A(A^TA)^{-1}A^T\mathbf{b}=P\mathbf{b}\\ P=A(A^TA)^{-1}A^T$$

  • Definition 20.10 (Idempotent) $$A=A^2$$ Projection matrix is an idempotent matrix.

  • interpolation polynomial 插值多项式

  • Runge’s phenomenon 多 oscillations 的数据比较难找到((interpolation polynomial 插值多项式))

  • 

• Slide 21 - Orthogonality III Slide21.pdf

  • Definition 21.1 (Inner Product Space over Real Number Field)
    若有 Inner Product Operation 在 $$V$$ ，那么 $$V$$ 是 Inner Product Space

    • Inner Product

      • Definition:

        • Assign a real number $$\left< \mathbf{x},\mathbf{y}\right> $$ for each pair of vectors $$\mathbf{x},\mathbf{y}\in V$$

        • $$\left< \mathbf{x},\mathbf{x}\right> \ge 0$$ when $$\mathbf{x}=0$$ equal

        • $$\left< \mathbf{x},\mathbf{y}\right> =\left< \mathbf{y},\mathbf{x}\right> ,\forall \mathbf{x},\mathbf{y}\in V$$
        • $$\left< \alpha\mathbf{x}+\beta\mathbf{y},\mathbf{z}\right> =\alpha\left< \mathbf{x},\mathbf{z}\right> +\beta\left< \mathbf{y},\mathbf{z}\right> ,\forall \mathbf{x},\mathbf{y},\mathbf{z}\in V\text{ and }\alpha,\beta\in \R$$

      • Frobenius inner product: Inner Product defined on $$\R^{m\times n }$$ $$\left<A,B\right>=\sum\limits^{m}_{i=1}\sum\limits^{n}_{j=1}a_{ij}b_{ij}$$

        • $$\left< A,A\right> =\sum\limits^{m}_{i=1}\sum\limits^{n}_{j=1}{a_{ij}}^2\ge 0$$ , $$a_{ij}=0$$ 取等

        • $$\left< A,B\right> =\left< B,A\right> $$
        • $$\left< \alpha A+\beta B,C\right> =\alpha\left< A,C\right> +\beta\left< B,C\right> $$

      • Inner Product on the vector space $$C[a,b]$$ : $$\left< f,g\right> =\int_a^b{f(x)g(x)dx}$$

        • $$\left< f,f\right> =\int_a^bf^2(x)dx\ge0$$ , $$f(x)\equiv 0$$ 取等

        • $$\left< f,g\right> =\left< g,f\right> $$
        • $$\left< \alpha f+\beta g,h\right> =\alpha\left< f,g\right> +\beta\left< g,h\right> $$

  • Definition 21.2 (Length of the vector in inner product space) $$||\mathbf{v}||=\sqrt{\left< \mathbf{v},\mathbf{v}\right> }$$

    • $$\forall \mathbf{x}\in \R^n,\ ||x|| = \sqrt{\mathbf{x}^T\mathbf{x}}$$
    • $$\forall f(x)\in C[a,b], ||f||={(\int_a^bf^2(x)dx)}^{\frac{1}{2}}$$
    • $$\forall A\in\R^{m\times n},||A||={(\sum\limits^m_{i=1}\sum\limits^n_{j=1}{a_{ij}}^2)}^{\frac{1}{2}}$$

  • Definition 21.3 (Orthogonal in the Inner Product Space) $$\left< \mathbf{x},\mathbf{y}\right> =0$$

  • Theorem 21.4 (Pythagorean’s Law for inner product space) $$||\mathbf{u}+\mathbf{v}||^2=||\mathbf{u}-\mathbf{v}||^2=||\mathbf{u}||^2+||\mathbf{v}||^2$$

  • Theorem 21.5 (Cauchy-Schwartz Inequality) $$|\left< \mathbf{u},\mathbf{v}\right> |\le||\mathbf{u}||\ ||\mathbf{v}||$$

  • Definition 21.6 (Normed Vector Space)

    • Norm: A real number $$||\mathbf{v}||\in \R$$ is the norm of $$\mathbf{v}$$

    • $$||\mathbf{v}||\ge 0$$ with equality if and only if $$\mathbf{v}=0$$
    • $$||\alpha\mathbf{v}||=|\alpha|\ ||\mathbf{v}||$$ for any scalar $$\alpha$$
    • $$||\mathbf{u}+\mathbf{v}||\le||\mathbf{u}||+||\mathbf{v}||$$ for any $$\mathbf{u},\mathbf{v}\in V$$

  • Theorem 21.7 (Norm on the Inner Product Space) $$||\mathbf{v}||=\sqrt{\left< \mathbf{v},\mathbf{v}\right> }$$ defines a norm on $$V$$

  • Definition 21.8 (Orthogonal Set) 一个集合，任取两不同向量 Inner Product 都为 0，那么集合叫 Orthogonal Set

  • Definition 21.9 (Orthonormal Set) 一个由 Unit Vectors 组成的 Orthogonal Set，Unit Vector 是说这个 Vector 的 norm 是 1

  • Theorem 21.10 (Orthogonal set are linearly independent)

    • Remark 1: Linear Independent 不能推出 Orthogonal

    • Remark 2: The set $$\{\mathbf{v}_1, \mathbf{v}_2, \cdots, \mathbf{v}_n\}$$ is orthonormal if and only if $$\delta_{ij} =\left< \mathbf{v}_i,\mathbf{v}_j\right> =\begin{cases} 1 & \text{if}\ i=j,\\ 0 & \text{if}\ i\neq j. \end{cases}$$

    • Remark 3: Orthogonal 转 Orthonormal (Normalization) $$\{\mathbf{u}_1, \mathbf{u}_2, \cdots, \mathbf{u}_n\} \Rightarrow \{\frac{\mathbf{u}_1}{||\mathbf{u}_1||}, \frac{\mathbf{u}_2}{||\mathbf{u}_2||}, \cdots, \frac{\mathbf{u}_n}{||\mathbf{u}_n||}\} $$

  • Definition 21.12 (Orthonormal Basis) $$\{\mathbf{u}_1,\cdots,\mathbf{u}_m\}$$ 是 orthonormal 的且 $$V=Span(\mathbf{u}_1,\cdots,\mathbf{u}_m)$$

  • Theorem 21.13 (Coordinate w.r.t orthonormal basis)
    Inner Product Vector Space $$V$$ 有 Orthonormal Basis $$\{\mathbf{u}_1,\cdots,\mathbf{u}_m\}$$ ， $$\mathbf{v}\in V$$ 满足 $$\mathbf{v}=\sum\limits_{i=1}^m\left< \mathbf{v},\mathbf{u}_i \right> \mathbf{u}_i$$

    • Inner Product Vector Space $$V$$ 有 Orthogonal Basis $$\{\mathbf{u}_1,\cdots,\mathbf{u}_m\}$$ ，则 $$\mathbf{v}\in V$$ 满足 $$\mathbf{v}=\sum\limits_{i=1}^m\frac{\left< \mathbf{v},\mathbf{u}_i\right> }{||\mathbf{u}_i||^2}\mathbf{u}_i$$

  • Property 21.18(Properties for orthogonal matrix)

    • Definition 21.15 (Orthogonal Matrix) $$Q\in \R^{n\times n}$$ ，若 $$Q$$ 的列向量是 $$\R^n$$ 中的一个OrthonormalSet，则 $$Q$$ 是OrthogonalMatrix

    • Theorem 21.16 (Equivalent Condition for Orthogonal Matrix)
      Orthogonal Matrix IFF $$Q^{-1}=Q^T$$

    • $$Q^TQ=I_n$$
    • $$\left< Q\mathbf{x},Q\mathbf{y}\right> =\left< \mathbf{x},\mathbf{y}\right> \\ \left< Q\mathbf{x},Q\mathbf{y}\right> =(Q\mathbf{y})^TQ\mathbf{x}=\mathbf{y}^TQ^TQ\mathbf{x}=\mathbf{y}^T\mathbf{x}=\left< \mathbf{x},\mathbf{y}\right> $$
    • $$||Q\mathbf{x}||=||\mathbf{x}||$$

  • Theorem 21.5 (Cauchy-Schwartz Inequality)
    If $$\mathbf{u},\mathbf{v}\in V$$ ( $$V$$ Inner Product Space), we have $$|\left< \mathbf{u},\mathbf{v}\right> |\le||\mathbf{u}||\ ||\mathbf{v}||$$

• Slide 22 - Orthogonality IV Slide22.pdf

  • Lemma 22.1 (Projection onto a subspace)
    Inner Product Space $$V$$ 内有 $$\{\mathbf{u}_1,\cdots,\mathbf{u}_m\}$$ 有 是 Subspace $$S$$ 的 Orthonormal Basis，对于任意 $$\mathbf{x}\in V$$ ，我们可以把 $$\mathbf{x}$$ 投影到 $$S$$ (即使 $$\mathbf{x}-\mathbf{p}\perp S$$ )，那么我们有 $$\mathbf{p}=\sum\limits^m_{i=1}\left< \mathbf{x},\mathbf{u}_i\right> \mathbf{u}_i$$

    • 参考((Theorem 21.13 (Coordinate w.r.t orthonormal basis)
      Inner Product Vector Space $$V$$ 有 Orthonormal Basis $$\{\mathbf{u}_1,\cdots,\mathbf{u}_m\}$$ ， $$\mathbf{v}\in V$$ 满足 $$\mathbf{v}=\sum\limits_{i=1}^m\left< \mathbf{v},\mathbf{u}_i \right> \mathbf{u}_i$$ ))，若是在这个空间内的向量用这个式子表示就可以直接表示。若是本来不在这个空间的向量，用这个式子表示就是投影。这是因为 $$\left< \mathbf{x}-\mathbf{p},\mathbf{u}_i\right> =0$$

  • Gram-Schmidt Process 格拉姆-施密特正交化

    • 使得一个 linearly independent 的向量集变为一个 orthonormal set 的同时维持 Span 不变

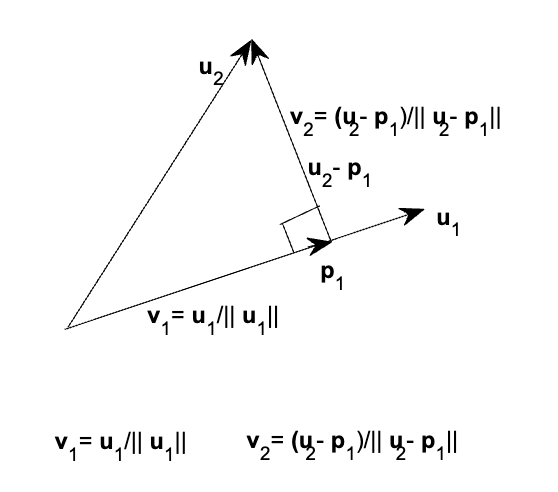    • 二维空间图示

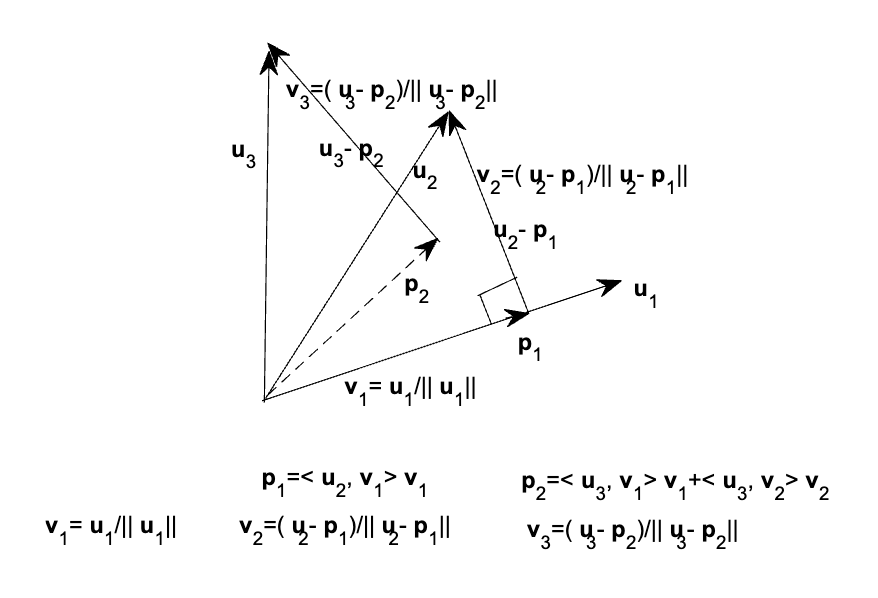    • 三维空间图示

    • 步骤：

      • $$\mathbf{v}_1=\frac{\mathbf{u}_1}{||\mathbf{u}_1||}$$

      • Project $$\mathbf{u}_2$$ onto $$Span(\mathbf{v}_1)$$ ， $$\mathbf{p}_1=\left< \mathbf{u}_2,\mathbf{v}_1\right> \mathbf{v}_1$$ ， $$\mathbf{v}_2=\frac{\mathbf{u}_2-\mathbf{p}_1}{||\mathbf{u}_2-\mathbf{p}_1||}\perp Span(\mathbf{v}_1)$$ *Now $$Span(\mathbf{v}_1,\mathbf{v}_2)=Span(\mathbf{u}_1,\mathbf{u}_2)$$

      • …

      • Project $$\mathbf{u}_m$$ onto $$Span(\mathbf{v}_1,\cdots,\mathbf{v}_{m-1})$$ ， $$\mathbf{p}_{m-1}=\left< \mathbf{u}_m,\mathbf{v}_1\right> \mathbf{v}_1+\left< \mathbf{u}_m,\mathbf{v}_2\right> \mathbf{v}_2+\cdots+\left< \mathbf{u}_m,\mathbf{v}_{m-1}\right> \mathbf{v}_{m-1}$$ $$\mathbf{v}_m=\frac{\mathbf{u}_m-\mathbf{p}_{m-1}}{||\mathbf{u}_m-\mathbf{p}_{m-1}||}\perp Span(\mathbf{v}_1,\cdots,\mathbf{v}_{m-1})$$ *Now $$Span(\mathbf{u}_1,\cdots,\mathbf{u}_{m})=Span(\mathbf{v}_1,\cdots,\mathbf{v}_{m})$$

  • Theorem 22.5 (QR decomposition) $$A=QR\\ (A\in \R^{m\times n}\ \text{rank}(A)=n\\ \text{i.e. Column Vectors Linearly Independent}\\ Q\in \R^{m\times n}\ \text{Orthogonal Column Vectors}\\ R\in \R^{n\times n}\ \text{Upper Triangular, Diagonal Positive})$$ Q 是经Gram-Schmidt 得到的，R用下面方法求

    • $$R=Q^{-1}A=Q^TA$$

    • Theorem: $$A^TA\hat{x}=A^T{\bf b}$$ $$R^TR\hat{x}=R^TQ^Tb$$ Finally: $$R\hat{x}=Q^T\mathbf{b}$$ $$\hat{x}=R^{-1}Q^T\mathbf{b}$$

• Slide 23 - Eigenvalues Slide23.pdf

  • Definition 23.1 (Eigenvalue and eigenvectors)
    Scalar $$\lambda$$ , Nonzero Vector $$\mathbf{x}$$ , Square Matrix $$A$$ , $$A\mathbf{x}=\lambda\mathbf{x}$$ $$\lambda$$ 叫作 eigenvalue (characteristic value), $$\mathbf{x}$$ 叫做 eigenvector (characteristic vector) w.r.t $$\lambda$$

    • 若 $$\mathbf{u}$$ 是关于 eigenvalue $$\lambda$$ 的 eigenvector, $$\alpha\mathbf{u}\ (\alpha\neq 0)$$ 也是

    • 若 $$\lambda$$ 是 $$A$$ 的 eigenvalue, 那么 $$\lambda^s$$ 是 $$A^S$$ 的 eigenvalue

  • Theorem 23.3 $$A\in \R^{n\times n}(\Complex^{n\times n})\ \lambda\in\R(\Complex)$$ 以下命题等效

    • $$\lambda$$ 是 $$A$$ 的 eigenvalue

    • $$(A-\lambda I)\mathbf{x}=\mathbf{0}$$ has nontrivial solutions. (As $$\lambda\mathbf{x}=\lambda I\mathbf{x}$$ and $$A\mathbf{x}=\lambda\mathbf{x}$$ )

    • $$\text{Null}(A-\lambda I)\neq\{\mathbf{0}\}$$ where $$\text{Null}(A-\lambda I)$$ is called the eigenspace corresponding to $$\lambda$$ , is subspace of $$\R^n(\Complex^n)$$ when $$\lambda\in\R(\Complex)$$

    • $$A-\lambda I$$ is singular

    • $$\text{det}(A-\lambda I)=0$$

      • A method to calculate the eigenvalues

      • $$\lambda$$ 同时是 $$A$$ 和 $$A^T$$ 的 eigenvalue

  • Definition 23.4 (Characteristic Polynomial) $$p_A(\lambda)=\text{det}(A-\lambda I)$$ is called the characteristic polynomial of $$A$$ . $$p_A(\lambda)=0$$ is called the characteristic equation of $$A$$ .

  • Theorem 23.9 (Fundamental theorem in Algebra)
    每个 $$n$$ 次系数可为复数的多项式有 $$n$$ 个复数根

    • 每个 $$n\times n$$ 的矩阵有 $$n$$ 个 eigenvalues

  • Theorem 23.10 (Product and Sum of Eigenvalues) $$A\in\R^{n\times n}(\Complex^{n\times n})\ \ \lambda_i\ \text{eigenvalues}$$ then: $$\displaystyle\text{det}(A)=\prod_{i=1}^n \lambda_i$$ $$\displaystyle\sum_{i=1}^n a_{ii}=\sum_{i=1}^n\lambda_i=tr(A)$$

    • $$\displaystyle \text{Trace}(A)= tr(A)= \sum_{i=1}^n a_{ii}$$
    • $$A\text{ is nonsingular}\iff \text{det}(A)\neq 0\iff\text{all eigenvalues }\lambda_i\neq 0$$
    • $$A$$ is nonsingular and $$\lambda$$ is the eigenvalue of $$A$$ , Then $$\iff \lambda^{-1}$$ is the eigenvalue of $$A^{-1}$$

  • Theorem 23.12 (Similar Matrices Have the Same Eigenvalues) $$B=S^{-1}AS$$ Then $$p_B(\lambda)=p_A(\lambda)$$

• Slide 24 - Diagonalization and Spectral Theorem Slide24.pdf

  • Definition 24.1 (Diagonalizable) $$A\in\R^{n\times n}$$ is diagonalizable if $$\exist X(X\text{ nonsingular}),\ X^{-1}AX=D$$ $$A=XDX^{-1}$$ , $$X$$ diagonalizes $$A$$

  • Theorem 24.2 (Eigenvectors belonging to distinct eigenvalues are linearly independent) $$\lambda_1, \lambda_2,\cdots,\lambda_k$$ are distinct eigenvalues of $$n\times n$$ matrix $$A$$ , $$\mathbf{x}_1, \mathbf{x}_2,\cdots,\mathbf{x}_k$$ are eigenvectors corresponding to $$\lambda_1, \lambda_2,\cdots,\lambda_k$$ , the $$\mathbf{x}_1, \mathbf{x}_2,\cdots,\mathbf{x}_k$$ are linearly independent

  • Theorem 24.3 (Sufficient and Necessary Condition for Diagonalization)
    A $$n\times n$$ matrix $$A$$ is diagonalizable iff $$A$$ has $$n$$ linearly independent eigenvectors

    • $$A$$ diagonalizable, column vectors of the diagonalizing matrix $$X$$ are eigenvectors of $$A$$ and the diagonal elements of $$D$$ are the corresponding eigenvalues

    • Diagonalizing Matrix $$X$$ is not unique
      Get a new one by reordering the columns or multiplying nonzero scalars for columns on an existing one

    • $$A^2=XD^2X^{-1},\ A^k=XD^kX^{-1}$$

  • Theorem 24.7 $$A\in \R^{n\times n}\text{ symmetric, eigenvals }\lambda_1,\cdots,\lambda_n\to$$ $$1.\ \lambda_i\in\R\\ 2.\ \lambda_i\ne\lambda_j\to \mathbf{x}_i,\mathbf{x}_j\text{ orthogonal (corresponding eigenvecs)}$$

  • Theorem 24.8 (Spectral Theorem (eigen decomposition theorem) for Real Symmetric Matrix) $$A$$ real symmetric, $$\exist Q\text{ orthogonal, }Q^{-1}AQ=Q^TAQ=\bigwedge(\text{diagonal})$$ $$Q$$ diagonalizes $$A$$
    求 $$\bigwedge$$ 的方法： $$\left[\begin{matrix}\lambda_1&0&0\\0&\lambda_2&0\\0&0&\lambda_3\end{matrix}\right]$$ 求 $$Q$$ 的方法：把 eigenvalue 对应的 eigenvector 作为列向量组成矩阵

    • Eigendecomposition or Eigenvalue Decomposition $$A=Q\bigwedge Q^T=\lambda_1\mathbf{q}_1\mathbf{q}_1^T+\cdots+\lambda_n\mathbf{q}_n\mathbf{q}_n^T$$

• Slide 25 - Quadratic Form Slide25.pdf

  • Definition 25.1 (Quadratic Equation with two unknowns) $$ax^2+2bxy+cy^2+dx+ey+f=0 (*)\to\\ \left[\begin{matrix}x &y\end{matrix}\right]\left[\begin{matrix}a&b\\b&c\end{matrix}\right]\left[\begin{matrix}x\\y\end{matrix}\right]+\left[\begin{matrix}d&e\end{matrix}\right]\left[\begin{matrix}x\\y\end{matrix}\right]+f=0$$ $$\mathbf{x} = \begin{bmatrix} x \\ y \end{bmatrix}, \quad A = \begin{bmatrix} a & b \\ b & c \end{bmatrix}$$ $${\bf x}^{T}A{\bf x}+[d,e{]{\bf x}+{f}=0}\to (*)$$

    -> $${\bf x}^TA{\bf x}$$ is the quadratic form with quadratic equation $$(*)$$ . The graph of $$(*)$$ is called theconic section

  • Definition 25.3 (Definite quadratic form and definite matrix) $${\bf x}\in\R^n,\,A\in\R^{n\times n}$$ symmetric $$f({\bf x})={\bf x}^TA{\bf x}$$

    • The quadratic form $$f({\bf x})$$ ispositive definiteif $$f({\bf x})\gt 0$$ for any $${\bf x \neq 0}$$ . $$A$$ is calledpositive definite matrix.

    • The quadratic form $$f({\bf x})$$ ispositive semidefiniteif $$f({\bf x})\ge 0$$ for any $${\bf x \neq 0}$$ . $$A$$ is calledpositive semidefinite matrix.

    • The quadratic form $$f({\bf x})$$ isindefinite if $$f({\bf x})$$ takes diff signs.

    • The quadratic form $$f({\bf x})$$ isnegative definiteif $$f({\bf x})\lt 0$$ for any $${\bf x \neq 0}$$ . $$A$$ is callednegative definite matrix.

    • The quadratic form $$f({\bf x})$$ isnegative semidefiniteif $$f({\bf x})\le 0$$ for any $${\bf x \neq 0}$$ . $$A$$ is callednegative semidefinite matrix.

  • MAT 2040’s Last Theorem $$A\in\R^{n\times n}$$ the following are eq:

    • $$A$$ is positive definite

    • All eigenvalues of $$A$$ are positive

    • The leading principal minors are positive

      • Leading principal minor: $$det(\text{leading principal submatrix})$$

      • Leading Principal Submatrix, 从左上角切小矩阵，例 $$A=\left[\begin{matrix}1&2&3\\4&5&6\\7&8&9\end{matrix}\right]\\ A_1=\left[\begin{matrix}1\end{matrix}\right]\\ A_2=\left[\begin{matrix}1&2\\4&5\end{matrix}\right]\\ A_3=\left[\begin{matrix}1&2&3\\4&5&6\\7&8&9\end{matrix}\right]$$

    • $$A=C^2$$ with $$C\gt 0$$
      • (Square root $$C=A^{1\over 2}=\sqrt{A}$$ )

    • $$A=LL^T$$ with $$L$$ being a lower triangular matrix with $$l_{ii}\gt 0\ (i=1,\cdots,n)$$ (Cholesky 分解)

    • $$A=LDL^T$$ $$L$$ unit lower triangular $$D\gt0$$ diagonal